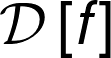Introdução ao Manifold Learning
Contents
7. Introdução ao Manifold Learning¶
7.1. Geometria dos dados¶
Muito do trabalhado de um Cientista de Dados não está apenas em criar sistemas de classificação, regressão ou recomendação. Aliás, estes são normalmente o resultado do fim de uma grande jornada aplicando diversas técnicas em cima dos dados coletados. Uma importante parte dessa jornada está em descobrir maneiras de compreender e utilizar a estrutura dos dados.
Eu tenho um carinho especial por esse tipo de abordagem. Minha formação é como físico e boa parte da compreensão que temos do Universo veio através dessa estrutura dos dados observados. Vou dar um exemplo: compreendemos o Universo como uma espécie de superfície (uma superfície complicada, mas ainda sim uma superfície), nós vivemos sobre ela e qualquer coisa que possamos fazer deve obedecer um conjunto de regras (Leis Físicas) que são determinadas, a grosso modo, pelo formato da superfície, ou seja, pela geometria. Se há uma estrela em determinado lugar, a massa dela curva o espaço e a regra a que estamos submetidos é ser atraído para a estrela.
O conjunto gigante de dados que observamos todos os dias pertence a algum universo próprio, com regras próprias e entender as regras desse ambiente nos permite entender como obter melhores respostas através dos dados. Temos hoje diversas maneiras de realizar este tipo de tarefa e aqui vou falar sobre uma chamada Manifold Learning ou Aprendizagem de Variedade. Primeiro precisamos entender o que é uma Variedade (Manifold em inglês).
7.2. Algumas definições¶
Essa parte pode parecer chata se você não gosta de matemática, mas é essencial definirmos alguns termos para compreender o que há pela frente.
Primeiro precisamos do conceito de mapa diferenciável (Um mapa é apenas uma definição mais abrangente de função):
Seja um mapa \(f:U \rightarrow V\), onde \(U \subset \mathbb{R}^{n}\) e \(V \subset \mathbb{R}^{k}\). Cada um deles, \(U\) e \(V\), é um subconjunto de algum espaço Euclidiano (dois espaços com dimensões não necessariamente iguais). Dizemos que o mapa \(f\) é suave ou diferenciável se para qualquer \(m\) as derivadas
formam um mapa suave, ou seja, se as derivadas existem em todos os pontos (não há divisões por zero ou descontinuidades).
Sejam \(X \subset \mathbb{R}^{n}\) e \(Y \subset \mathbb{R}^{k}\) subconjuntos quaisquer. O mapa \(f: X \rightarrow Y\) é suave se para cada \(x\in X\) existe uma vizinhança aberta \(U \subset \mathbb{R}^{n}\) (uma região de pontos vizinhos a \(x\) que não é um intervalo fechado) e um mapa suave \(g: U \rightarrow \mathbb{R}^{k}\) que coincida com \(f\) na intersecção \(U \cap X\). Isso basicamente quer dizer que pode não existir um único mapa que mapeie todos os pontos de \(X\) para \(Y\), mas se existir um conjunto de mapas que façam isso, então o conjunto é equivalente a um mapa suave.
Dizemos que um mapa \(f: X \rightarrow Y\) é um homeomorfismo se é uma bijeção com \(f\) e sua inversa \(f^{-1}\) contínuas. No caso de \(f\) e \(f^{-1}\) serem ambas suaves, dizemos que o homeomorfismo é um difeomorfismo.
Agora, uma variedade é um espaço topológico (basicamente um espaço em que conseguimos medir a distância entre dois pontos, pense em uma superfície qualquer) que localmente é difeomórfico a algum espaço Euclidiano, ou seja, há um conjunto de mapas capaz de projetar todos os pontos da variedade para o espaço Euclidiano que ao mesmo tempo possuem inversas contínuas e suaves. O termo localmente aqui significa na vizinhança de algum ponto.
A chave aqui está na curvatura desse espaço, podemos entender uma variedade como um espaço topológico que ao olhado de perto (dando um zoom) não veremos curvatura, será um plano.
Só nos falta agora a definição de variedade diferenciável. Seja \(M \subset \mathbb{R}^{n}\), \(M\) é uma variedade diferenciável de dimensão \(d\) se para cada ponto \(x \in M\) existir uma vizinhança aberta \(U\) contendo \(x\) e um difeomorfismo \(f:U \rightarrow V\) onde \(V \subset \mathbb{R}^{d}\). Essas vizinhanças são chamadas de patches coordenados e os difeomorfismos de cartas coordenadas (ou apenas sistemas de coordenadas, coordinate chart em inglês).
Vamos a um exemplo: Pense em um círculo desenhado em um plano. O círculo é uma superfície de dimensão 1 merguhada (embedded) dentro do plano de duas dimensões, o \(\mathbb{R}^{2}\). Cada um dos pontos desse círculo podem ser projetados no \(\mathbb{R}^{2}\) com as equações
funções do ângulo \(\theta\) e do raio \(r\). Para fazer a transformação inversa precisamos das equações
Observe que temos três possíveis mapas de \(\theta\) para que possamos cobrir todo o círculo, três patches e três funções. Os mapas podem não ser suaves em algum ponto, mas há outro mapa suave nesse ponto. Assim cobrimos tudo e o círculo dotado dessas projeções, ou mapas diferenciáveis formam uma variedade de dimensão 1 mergulhada em um espaço Euclidiano de dimensão 2.
7.3. Objetivo de Manifold Learning¶
De posse desses conceitos podemos entender um conceito bem famoso em Ciência de Dados chamado de Hipótese da Variedade. Ela afirma que os dados observados(quaisquer que sejam) pertencem à uma variedade, ou seja, são pontos coletados desta superfície e com um número suficiente de pontos podemos recriar a variedade ou aprender suas propriedades. É isso que chamamos de Manifold Learning.
Seja o dataset \(X = \lbrace x_{1}, ..., x_{n}\rbrace \subset \mathbb{R}^{D}\), cada data point \(x\) é um vetor de dimensão \(D\) (as vezes chamado de vetor de features). Assumimos que os dados pertencem à uma variedade de dimensão \(d\) mergulhada em \(\mathbb{R}^{D}\), onde \(d < D\).
A tarefa que queremos realizar é: Dado que \(X \subset \mathbb{R}^{D}\) tal que \(X \subset M\), encontre a estrutura da variedade \(M\), isto é, a coleção de patches coordenados e cartas coordenadas.
Os patches de um conjunto discreto são construídos encontrando os \(k\) vizinhos mais próximos (knn, k-nearest neighbors) de cada ponto \(x \in X\).
Dados os patches o objetivo é descobrir os difeomorfismos:
ou seja, as funções que mapeiam \(x\) e seus vizinhos para vizinhanças mergulhadas no \(\mathbb{R}^{k}\).
7.4. E agora?¶
Dado que tenhamos encontrado os difeomorfimos o que podemos fazer com eles?
Bom, uma aplicação bem famosa é forçar que os difeomorfismos tenham dimensões pequenas, como 2 ou 3, para que a variedade possa ser visualizada. Essa é uma aplicação de Redução de Dimensionalidade (Dimensionality Reduction).
Podemos ainda aplicar uma espécie de filtro que permita observar pedaços da variedade no formato de grafos e como ali se comportam o valor das features. Isso faz parte de uma área de estudo conhecida como Análise Topológica de Dados (Topolical Data Analysis).
Na minha humilde opinião as aplicações mais interessantes se encontram em aprender a estrutura da variedade de modo que possamos fazer amostragem (sampling) de sua pontos. As técnicas usadas para fazer isso são aquelas que usam modelos geradores como Generative Adversarial Networks , Variational Autoencoder e normalizing-flows.
Sobre as técnicas de manifold learning especificamente pretendo apresentar aqui futuramente.