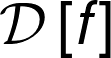The Multi-Armed Bandits: Exploitation vs Exploration
Contents
3. The Multi-Armed Bandits: Exploitation vs Exploration¶
3.1. 10-armed Testbed¶
Descrição do problema: …..
Estratégias: Near-Greedy, Optimistic, Upper-Confidence-bound Action Selection, Gradient Bandit Algorithms
Some definitions:
\(R_{t}\) - Reward received at time t
\(A_{t}\) - Action at time t
\(k\) - Number of possible actions
\(q(a)\) - Expected reward given that action a is chosen: \(q(a)\equiv \mathbb{E}[R_{t}|A_{t}=a]\)
\(Q_{t}(a)\) - Estimated value of action aat time t.
import numpy as np
import scipy as sp
import matplotlib.pyplot as plt
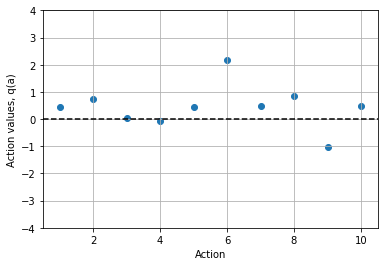
q = np.random.normal(0,1,(1,10))
plt.grid(True)
plt.scatter(np.arange(1,11),q[0,:])
plt.ylim(-4,4)
plt.xlim(0.5,10.5)
plt.plot([0.5,10.5],[0.,0],'--k')
plt.ylabel('Action values, q(a)')
plt.xlabel('Action')
def nearGreedy_plot(eps):
K = 2000
M = 1000
q = np.random.normal(0,1,(K,10))
Q = np.random.normal(0,1,(K,10))*0.00001
#Q[:,:]=5 # uncomment to change initial value
A = np.zeros([K,10])
R = np.zeros([K,10])
ER = np.zeros([1,K])
RT = np.zeros([1,K])
RTm = np.zeros([1,K])
ERm = np.zeros([1,K])
PAm = np.zeros([M])
for j in range(M):
PA = np.zeros([K])
for i in range(K):
if np.random.rand() < eps:
a = np.random.randint(0,10)
else:
a = np.argmax(Q[i,:])
A[i,a] = A[i,a] +1
R[i,a] = np.random.normal(q[i,a],1)
Q[i,a] = Q[i,a]+(1./A[i,a])*(R[i,a]-Q[i,a])
ER[0,i] = abs(Q[i,a]-q[i,a])
RT[0,i] = Q[i,a]
if a == np.argmax(q[i,:]):
PA[i] += 1
PAm[j] = np.sum(PA)/len(PA)
RTm = np.vstack([RTm,RT])
ERm = np.vstack([ERm,ER])
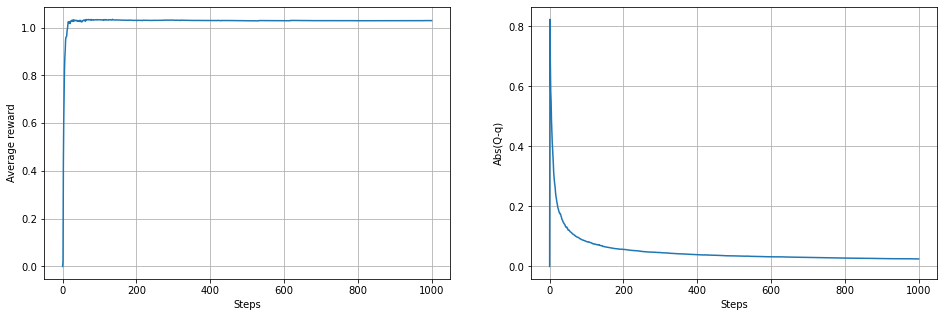
plt.figure(figsize=(16,5))
plt.subplot(1,2,1)
plt.plot(range(len(RTm)),np.mean(RTm,axis=1))
plt.grid(True)
plt.xlabel('Steps')
plt.ylabel('Average reward')
plt.subplot(1,2,2)
plt.plot(range(len(ERm)),np.mean(ERm,axis=1))
plt.grid(True)
plt.xlabel('Steps')
plt.ylabel('Abs(Q-q)')
plt.show()
plt.figure(figsize=(16,5))
plt.plot(range(len(PAm)),PAm*100)
plt.grid(True)
plt.xlabel('Steps')
plt.ylabel('Average % right choice')
plt.ylim(0,100)
plt.show()
nearGreedy_plot(0.0)
nearGreedy_plot(0.01)
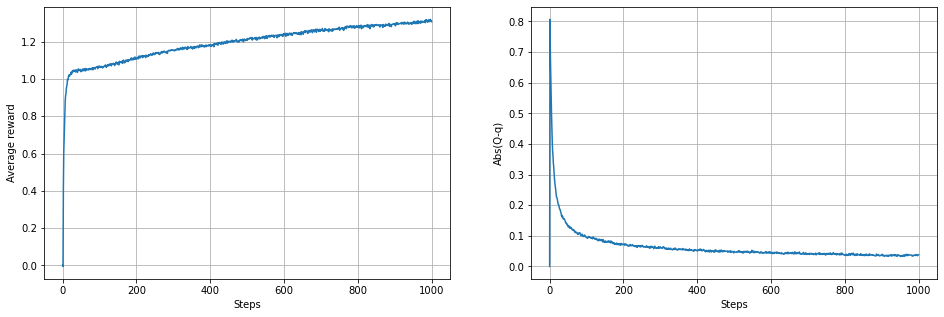
nearGreedy_plot(0.1)
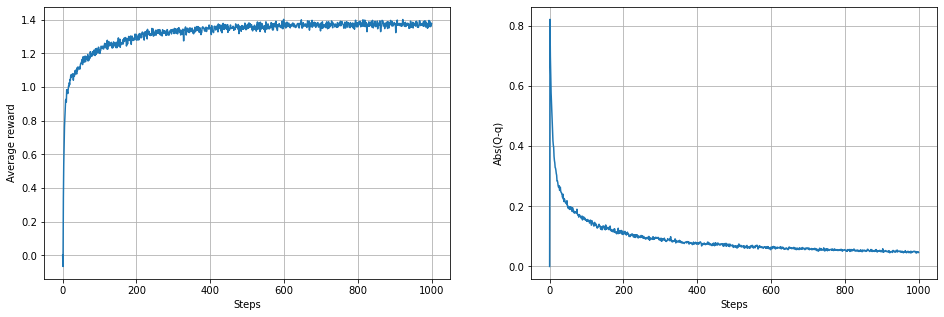
def nearGreedy(eps):
K = 2000
M = 1000
q = np.random.normal(0,1,(K,10))
Q = np.random.normal(0,1,(K,10))*0.00001
A = np.zeros([K,10])
R = np.zeros([K,10])
ER = np.zeros([1,K])
RT = np.zeros([1,K])
RTm = np.zeros([1,K])
ERm = np.zeros([1,K])
PAm = np.zeros([M])
for j in range(M):
PA = np.zeros([K])
for i in range(K):
if np.random.rand() < eps:
a = np.random.randint(0,10)
else:
a = np.argmax(Q[i,:])
A[i,a] = A[i,a] +1
R[i,a] = np.random.normal(q[i,a],1)
Q[i,a] = Q[i,a]+(1./A[i,a])*(R[i,a]-Q[i,a])
ER[0,i] = abs(Q[i,a]-q[i,a])
RT[0,i] = Q[i,a]
if a == np.argmax(q[i,:]):
PA[i] += 1
PAm[j] = np.sum(PA)/len(PA)
RTm = np.vstack([RTm,RT])
ERm = np.vstack([ERm,ER])
return RTm,ERm,PAm
def plotRT(A1,A2,A3,eps1,eps2,eps3):
plt.figure(figsize=(16,5))
plt.plot(range(len(A1)),np.mean(A1,axis=1),label = '$\epsilon$ = '+ str(eps1))
plt.plot(range(len(A2)),np.mean(A2,axis=1),label = '$\epsilon$ = '+ str(eps2))
plt.plot(range(len(A3)),np.mean(A3,axis=1),label = '$\epsilon$ = '+ str(eps3))
plt.legend(loc=0)
plt.grid(True)
plt.xlabel('Steps')
plt.ylabel('Average reward (epsilon)')
plt.ylim(0,1.55)
def plotER(A1,A2,A3,eps1,eps2,eps3):
plt.figure(figsize=(16,5))
plt.plot(range(len(A1)),np.mean(A1,axis=1),label = '$\epsilon$ = '+ str(eps1))
plt.plot(range(len(A2)),np.mean(A2,axis=1),label = '$\epsilon$ = '+ str(eps2))
plt.plot(range(len(A3)),np.mean(A3,axis=1),label = '$\epsilon$ = '+ str(eps3))
plt.legend(loc=0)
plt.grid(True)
plt.xlabel('Steps')
plt.ylabel('Abs(Q-q) (epsilon)')
plt.show()
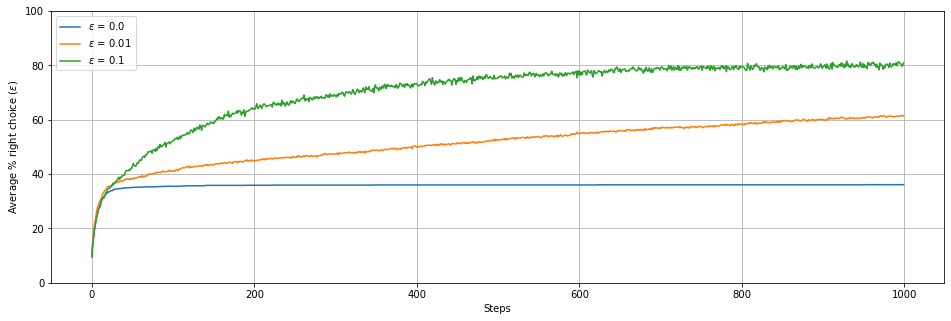
def plotPA(A1,A2,A3,eps1,eps2,eps3):
plt.figure(figsize=(16,5))
plt.plot(range(len(A1)),A1*100,label = '$\epsilon$ = '+ str(eps1))
plt.plot(range(len(A2)),A2*100,label = '$\epsilon$ = '+ str(eps2))
plt.plot(range(len(A3)),A3*100,label = '$\epsilon$ = '+ str(eps3))
plt.legend(loc=0)
plt.grid(True)
plt.xlabel('Steps')
plt.ylabel('Average % right choice ($\epsilon$)')
plt.ylim(0,100)
A1,B1,C1 = nearGreedy(0.0)
A2,B2,C2 = nearGreedy(0.01)
A3,B3,C3 = nearGreedy(0.1)
plotRT(A1,A2,A3,0.0,0.01,0.1)
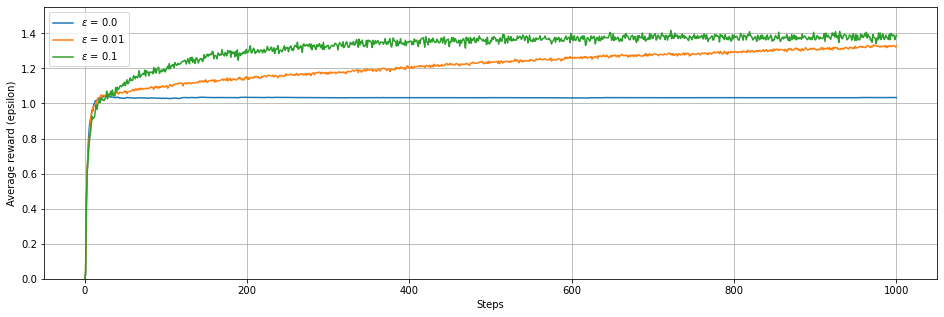
plotER(B1,B2,B3,0.0,0.01,0.1)
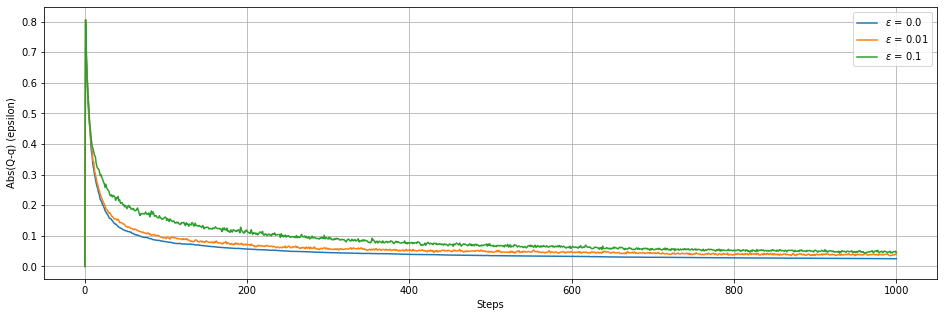
plotPA(C1,C2,C3,0.0,0.01,0.1)