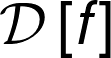2. Ranknet¶

The algorithm called Ranknet is a way to train a neural network to assign a score to an observation in almost the same way we did manually in the previous section.

Let \(\mathcal{D} = \{(\mathbf{x}_{i},y_{i}) | i \in \{1,2,...,N\}, \mathbf{x}_{i} \in \mathbf{X} \subset \mathbb{R}^{m} \text{ and } y_{i} \in \mathbb{R}^{1} \}\) be a dataset with \(m\) features, 1 label and \(N\) obervations.

Assuming we are solving a ranking problem, the label represents some kind of relevance. In this example we will assume that a label can have two values, \(\{0,1\}\). So the definition above is changed to \(y_{i} \in \{0,1\}\), where \(1\) means more relevance than \(0\). In future examples we will see other kinds of relevance.

To train a Ranknet one needs in each iteration to sample a pair of observations, one more relevant than the other. We will refer to them as:

\(\mathbf{x}_{i,r}\): features vector of observation \(i\) which has relevance \(r\).

Since we know the relevance of an observation in sampling stage, we will refer to a relevant observation as \(\mathbf{x}_{i,1}\) and \(\mathbf{x}_{i,0}\) to the non-relevant one.

If you do not like the indices you can think the relevance being the label, such that \(\mathbf{x}_{i,r}\) becomes the pair \(\left( \mathbf{x}_{i},y_{i} \right)\). It does not matter the way we identify the relevance of an observation, just remember, again, to sample two of them one more relevant than the other.

Basically our model will be a map \(f: \mathbf{X} \to \mathbb{R}^{1}\), i.e.,

\[f(\mathbf{x}_{i,r};\theta) = s_{i},\]

where \(\theta\) are the set of parameters we want the model to learn. After that we use the same procedure as before: compute likelihood for each pairs, use the log-likelihood as an error and use the \(\lambda{ij}\) to update the model. However, we still need to understand the lambdas.

2.1. The lambdas¶

We need to understand how to optimize our model. Our main resource is this nice paper by Christopher J.C. Burgers from Microsoft. So let us begin from the likelihood we already know, using a sigmoid function with parameters \(\alpha\) (the paper uses \(\sigma\) which could cause confusion, since usually people uses this symbol to the sigmoid function), such that the probability of item \(i\) should be ranked higher than item \(j\) is given by:

\[\sigma_{ij} = \sigma(s_{i},s_{j}) = \frac{1}{1 + e^{-\alpha(s_{i}-s_{j})}}\]

The model, \(f\), outputs the scores, \(s_{i}\) and \(s_{j}\) and the probability is computed with these outputs. Since this is a probability we can use cross-entropy as the loss function:

\[L = -P_{ij}\log{(\sigma_{ij})} - (1-P_{ij})\log{(1-\sigma_{ij})}\]

The quantity \(P_{ij}\) is the true probability of item \(i\) being ranked higher than item \(j\). Since in our modeling we are considering the first item always more relevant than the second, \(P_{ij}\) is always \(1\) and then we have simply the log-likelihood:

\[L = - \log{\left(1 + e^{-\alpha(s_{i}-s_{j})} \right)}.\]

This is the quantity we want to minimize during training and by using a gradient descent method we need the derivative of the loss w.r.t. the model parameters, \(\theta\) to update them:

\[\theta_{k} = \theta_{k} - \gamma \nabla_{\theta_{k}}L.\]

However, \(L\) is explicitly a function of the scores of two different observations, not of \(\theta_{k}\). Remember the loss is a functional of our model, usually represented as \(L\left[f(\cdot ; \theta_{k}) \right]\). Thus, we need to do the derivative of \(L\) w.r.t. \(\theta_{k}\) using the chain rule:

\[\nabla_{\theta_{k}} L = \frac{\partial L}{\partial \theta_{k}} = \frac{\partial L}{\partial f} \frac{\partial f}{\partial \theta_{k}}\]

Since \(s_{i} = f(\mathbf{x}_{i}; \theta_{k})\) we should write it considering both terms \(i\) and \(j\):

\[\nabla_{\theta_{k}} L = \frac{\partial L}{\partial s_{i}} \frac{\partial s_{i}}{\partial \theta_{k}} + \frac{\partial L}{\partial s_{j}} \frac{\partial s_{j}}{\partial \theta_{k}}\]

The derivatives \(\frac{\partial L}{\partial s_{i}}\) and \(\frac{\partial L}{\partial s_{j}}\) are easy to compute:

\[\frac{\partial L}{\partial s_{i}} = \frac{-\alpha}{1+e^{-\alpha(s_{i}-s_{j})}}e^{-\alpha(s_{i}-s_{j})} = \frac{-\alpha}{1+e^{\alpha(s_{i}-s_{j})}},\]

\[\frac{\partial L}{\partial s_{j}} = \frac{\alpha}{1+e^{\alpha(s_{i}-s_{j})}}.\]

They have the same intensity and oposite sign, \(\frac{\partial L}{\partial s_{i}} = - \frac{\partial L}{\partial s_{j}}\). We can now rewrite \(\nabla_{\theta_{k}} L\):

\[\begin{split} \begin{align} \nabla_{\theta_{k}} L &= \frac{-\alpha}{1+e^{\alpha(s_{i}-s_{j})}} \left(\frac{\partial s_{i}}{\partial \theta_{k}} - \frac{\partial s_{j}}{\partial \theta_{k}} \right)\\ &= \lambda_{ij}\left(\frac{\partial s_{i}}{\partial \theta_{k}} - \frac{\partial s_{j}}{\partial \theta_{k}} \right) \end{align}\end{split}\]

Now we see that the lambdas are also functionals of the model and they control the intensity of the update in \(\theta_{k}\). To complete the story we write the gradient descent full update as:

\[\theta_{k} = \theta_{k} - \gamma \lambda_{ij}\left(\frac{\partial s_{i}}{\partial \theta_{k}} - \frac{\partial s_{j}}{\partial \theta_{k}} \right).\]

These calculations are just to understand how the technique works, in practice if we use the cross-entropy loss function with an autograd framework like Tensorflow and Pytorch, it will automatically compute the lambdas for us.

2.2. Ranknet algorithm¶

The algorithm to train our neural network is the following:

Algorithm 2.1 (Ranknet algorithm)

Init weights \(\theta\) for model \(f\)

Repeat for T epochs:

Sample \(\mathbf{x}_{i,1},\mathbf{x}_{j,0} \sim \mathcal{D}\)
- Train and update \(f\):
  - Compute scores
    - \(s_{i,1} = f(\mathbf{x}_{i,1};\theta)\)
    - \(s_{j,0} = f(\mathbf{x}_{j,0};\theta)\)
  - Compute likelihood, \(\sigma(s_{i,1},s_{j,0})\)
    - \(prob = sigmoid(s_{i,1},s_{j,0})\)
  - Compute loss:
    - \(L \left( prob,1 \right)\)
  - Update \(f\):
    - \(\theta \leftarrow \theta - \gamma \nabla_{\theta_{k}}L\)

The parameter \(\gamma\) is the learning rate used to adjust the updating.

2.3. Building and training the ranknet¶

To train out model we will use the ranking teams dateset defined in the datasets section.

# Imports
import numpy as np
import pandas as pd

import torch
from torch.utils.data import Dataset, DataLoader
import torch.nn as nn
import torch.optim as optim
from torch.optim import lr_scheduler

ngpu=1
device = torch.device("cuda:0" if (torch.cuda.is_available() and ngpu > 0) else "cpu")

# loader function
class CustomDataset(Dataset):
    def __init__(self,x):
        self.x = torch.tensor(x,dtype=torch.float32)
        self.length = self.x.shape[0]

    def __getitem__(self,idx):
        return self.x[idx]
    def __len__(self):
        return self.length

def create_loader(x,workers,batch_size):
    dataset = CustomDataset(x)
    loader = DataLoader(dataset, 
                        batch_size=batch_size,
                        shuffle=True, 
                        num_workers=workers)
    return loader

# neural network architecture
class Net(nn.Module):
    def __init__(self,input_dim=13,hidden_dim=64,output_dim=1,ngpu=ngpu):
        super(Net, self).__init__()
        self.input_dim = input_dim
        self.output_dim = output_dim
        self.hidden1 = nn.Linear(self.input_dim, hidden_dim)
        self.hidden2 = nn.Linear(hidden_dim, hidden_dim//2)
        self.hidden3 = nn.Linear(hidden_dim//2, hidden_dim//4)
        self.out = nn.Linear(hidden_dim//4, self.output_dim)

    def forward(self, x):
        h = nn.Dropout(p=0.0)(torch.relu(self.hidden1(x)))
        h = nn.Dropout(p=0.0)(torch.relu(self.hidden2(h)))
        h = nn.Dropout(p=0.0)(torch.relu(self.hidden3(h)))
        return self.out(h)

# initialize weights
def init_weights(m):
    if type(m) == nn.Linear:
        torch.nn.init.xavier_normal_(m.weight).to(device)
        m.bias.data.fill_(0.001)
    
# function to define model
def define_model(input_dim=3,hidden_dim=64,output_dim=1,ngpu=ngpu):
    model = Net(input_dim,hidden_dim,output_dim).to(device)
    if (device.type == 'cuda') and (ngpu > 1):
        encoder = nn.DataParallel(encoder, list(range(ngpu)))
        decoder = nn.DataParallel(decoder, list(range(ngpu)))

    model.apply(init_weights)

    learning_rate, beta1, beta2 = [1e-4,0.9,0.999]
    eps,weight_decay,amsgrad = [1e-8,1e-3,False]
    optimizer = optim.Adam(params=model.parameters(),
                               lr=learning_rate,
                               betas=(beta1,beta2),
                               eps=eps,
                               weight_decay=weight_decay,
                               amsgrad=amsgrad)
    return model,optimizer

# function to split observations of X in (X_relevant,X_irrelevant)
def build_data_batch(X):
    rel_data = X[:,:input_dim].to(device)
    irel_data = X[:,input_dim:].to(device)
    return rel_data,irel_data

def ones_tensor(data_size):
    return torch.ones((data_size,1)).to(device)

# training function
def train_model(model,optimizer,loader,scheduler,epochs):
    loss_his = []
    loss_func = nn.BCELoss()
    for epoch in range(1,epochs+1):
        loss_ = []
        for i, X_train in enumerate(loader):
            rel_train,irel_train = build_data_batch(X_train)
            ones = ones_tensor(rel_train.shape[0])
            probs = torch.sigmoid(model(rel_train)-model(irel_train))
            loss = loss_func(probs,ones)
            loss.backward()
            optimizer.step()
            optimizer.zero_grad()
            loss_his.append(loss.item())
        scheduler.step()
        if epoch%10 == 0:
            print(f"{epoch}| Train loss: {loss.item():.6f}")
    return model,loss_his

team_df = pd.read_csv("data/ranking-teams-simulated.csv")

workers      = 12
batch_size   = 13
input_dim,hidden_dim,output_dim = [7,100,1]
train_data = np.load("data/ranking-teams.npy")
train_loader = create_loader(train_data,workers,batch_size)

model,optimizer = define_model(input_dim,hidden_dim,output_dim,ngpu)
lambda1 = lambda epoch: 0.95 ** epoch
scheduler = lr_scheduler.LambdaLR(optimizer,lr_lambda=[lambda1],verbose=False)

model,loss_his = train_model(model,optimizer,train_loader,scheduler,100)
>>> 10| Train loss: 0.671339
>>> 20| Train loss: 0.570556
>>> 30| Train loss: 0.473807
>>> 40| Train loss: 0.620052
>>> 50| Train loss: 0.625935
>>> 60| Train loss: 0.556643
>>> 70| Train loss: 0.431248
>>> 80| Train loss: 0.573984
>>> 90| Train loss: 0.695569
>>> 100| Train loss: 0.452465

def compute_ranknet_scores(team_df,model):
    x = torch.tensor(team_df[["att","def","sta","coa","int","cre","luc"]].values,dtype=torch.float32).reshape(len(team_df),7).to(device)
    return model(x).detach().cpu().numpy()

team_df["score"] = compute_ranknet_scores(team_df,model)
team_df.sort_values(by="score",ascending=False)

	att	def	sta	coa	int	cre	luc	potential	points	score
12	2	4	3	6	6	6	2	109.2	21	5.989317
2	2	4	3	7	2	2	3	96.4	21	5.782486
19	4	5	3	4	3	2	5	93.4	20	5.415341
23	2	2	4	5	5	4	3	81.0	21	5.030266
7	3	3	2	4	3	4	3	66.6	17	4.731111
3	3	2	4	5	2	4	2	71.0	16	4.628915
5	3	2	6	5	1	2	3	78.0	13	4.438781
0	5	2	4	4	2	3	2	68.4	18	4.388402
15	5	2	4	5	2	2	1	73.0	16	4.325098
11	5	2	3	2	5	6	3	73.4	14	4.299539
21	2	1	2	3	1	4	5	55.6	14	4.147776
9	3	1	5	6	3	1	1	57.2	13	4.049124
25	4	6	2	1	9	2	3	53.0	13	3.906338
17	3	1	2	4	5	4	1	45.4	11	3.904254
18	1	1	2	3	3	6	2	41.4	9	3.713337
10	2	2	3	3	6	2	3	51.0	10	3.548511
8	1	3	2	2	4	2	5	43.2	11	3.541099
22	5	2	2	1	1	5	3	42.8	10	3.459270
1	2	3	3	2	1	5	3	51.2	11	3.409286
24	3	1	5	3	6	3	1	47.1	11	3.375598
4	5	5	3	1	1	3	3	38.5	6	3.245562
6	3	1	3	3	4	2	1	34.9	6	3.052202
16	1	1	4	3	3	2	3	33.6	5	3.040318
14	2	1	4	4	2	1	1	30.4	6	2.973052
13	1	2	3	2	1	3	3	32.2	8	2.743444
20	2	4	2	2	4	1	2	32.8	4	2.699513

corr = team_df[["potential","points","score"]].corr("spearman")
corr

	potential	points	score
potential	1.000000	0.941811	0.951453
points	0.941811	1.000000	0.950738
score	0.951453	0.950738	1.000000

def dcg(r,i):
    return (2**r - 1)/(np.log2(1+i))

def dcg_k(x,k):
    result = 0
    for i in range(1,k+1):
        result += dcg(x[i-1],i)
    return result

def max_dcg_k(x,k):
    x = sorted(x)[::-1]
    return dcg_k(x,k)

def ndcg_k(x,k):
    return dcg_k(x,k)/max_dcg_k(x,k)

ndcg_list = []
for col in ["potential","points","score","att","def","sta","coa","int","cre","luc"]:
    ndcg_list.append([col]+[ndcg_k(team_df.sort_values(by=col,ascending=False)["potential"].values,k) for k in [3,10,20,26]])

ndcg_df = pd.DataFrame(ndcg_list,columns=["feat"]+[f"ndcg_{k}" for k in [3,10,20,26]])

ndcg_df[ndcg_df["feat"].isin(["potential","points","score"])]

	feat	ndcg_3	ndcg_10	ndcg_20	ndcg_26
0	potential	1.000000	1.000000	1.000000	1.000000
1	points	0.500092	0.500099	0.500099	0.500099
2	score	1.000000	1.000000	1.000000	1.000000

ndcg_df[ndcg_df["feat"].isin(["att","def","sta","coa","int","cre","luc"])]

	feat	ndcg_3	ndcg_10	ndcg_20	ndcg_26
3	att	1.106776e-11	0.000006	0.239830	0.239830
4	def	8.763021e-06	0.430698	0.430698	0.430698
5	sta	4.053424e-10	0.289037	0.289075	0.289075
6	coa	5.000916e-01	0.500092	0.500096	0.500096
7	int	1.371780e-17	0.430635	0.430671	0.430671
8	cre	9.999028e-01	0.999903	0.999907	0.999938
9	luc	1.105770e-05	0.000011	0.244673	0.244673

Disorder Transform

Ranknet

Contents

2. Ranknet¶

2.1. The lambdas¶

2.2. Ranknet algorithm¶

2.3. Building and training the ranknet¶