.ipynb .pdf

repository open issue

Binder

Contents

4. Maximum Likelihood Estimation

This a procedure or a method to find the parameters which maximize the likelihood. Let \(\theta\) be a parameter of a distribution that generates \(x\), \(p(x | \theta)\). This is the likelihood is the Bayes rule:

\[p(\theta | x) = \frac{p(x | \theta) p(\theta)}{p(x)}\]

So, we want to know what is the value os \(\theta\) which gives the maximum value of the likelihood for our observed data \(x\). The likelihood function is:

\[L(\theta,X) = p(X | \theta) = \prod_{i=1}^{N} p(x_{i} | \theta).\]

The log-likelihood is:

\[\mathcal{L}(\theta,X) = \ln{L}(\theta,X) = \sum_{i=1}^{N} \ln{p(x_{i} | \theta)}\]

and we want:

\[\theta_{ml} = argmax_{\theta} L(\theta,X).\]

For known distributions it is possible to find closed forms for the estimator. When that is the case we can find the critical point setting

\[\frac{\partial \mathcal{L}(\theta,X)}{\partial \theta} = 0\]

and solve it for \(\theta\).

Let us try an example.

4.1. Maximum Likelihood Estimation for Bernoulli distribution

\(Bernoulli(x | \theta) = p(x | \theta) = \theta^{x}(1-\theta)^{1-x}\) where \(x \in \lbrace 0,1 \rbrace\)

\[L(\theta,X) = \prod_{i=1}^{N}\theta^{x_{i}}(1-\theta)^{1-x_{i}}\]

\[\mathcal{L}(\theta,X) = \sum_{i=1}^{N}\ln{\theta^{x_{i}}} + \sum_{i=1}^{N}(1-\theta)^{1-x_{i}} = \ln{\theta}\sum_{i=1}^{N}x_{i} + \ln{(1-\theta)}\sum_{i=1}^{N}1-x_{i}\]

\[\frac{\partial \mathcal{L}(\theta,X)}{\partial \theta} = \frac{1}{\theta}\sum_{i=1}^{N}x_{i} - \frac{1}{1-\theta}\sum_{i=1}^{N}(1-x_{i})=0\]

Solving it we have

\[\theta_{ml} = \frac{1}{N}\sum_{i=1}^{N}x_{i}\]

This is the maximum likelihood estimator of the Bernoulli distribution parameter \(\theta\).

4.2. Simple example of maximum likelihood by brute force

import numpy as np
from scipy.stats import norm,crystalball
import matplotlib.pyplot as plt

def _compute_loglikelihood(model,x):
    return -np.mean(model.logpdf(x))

def compute_loglikelihood(param_vector,x):
    result = {}
    for item in param_vector:
        py = norm(loc=item,scale=0.4)
        result[item] = _compute_loglikelihood(py,x)
    return result

def find_best_param(result,first=True):
    flag = 0 if first==True else -1
    x = sorted(result.items(), key=lambda item: item[1])[flag]
    return {x[0]:x[1]}

px = norm(loc=0,scale=0.5)
x = px.rvs(size = 100)
result = compute_loglikelihood([-1,-0.5,0.1,0.3,1.0],x)
μ = find_best_param(result)
py = norm(loc=list(μ.keys())[0],scale=0.4)
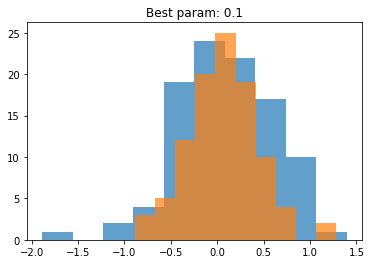
plt.title(f"Best param: {list(μ.keys())[0]}")
plt.hist(x,label="data",alpha=0.7)
plt.hist(py.rvs(100),label="model",alpha=0.7)
plt.show()

px = crystalball(beta=1.5,m=2.5,loc=0,scale=0.5)
x = px.rvs(size = 100)
result = compute_loglikelihood([-1,-0.5,0.1,0.3,1.0],x)
μ = find_best_param(result)
py = norm(loc=list(μ.keys())[0],scale=0.4)
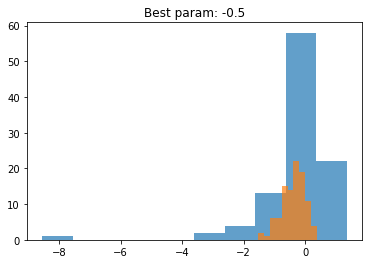
plt.title(f"Best param: {list(μ.keys())[0]}")
plt.hist(x,label="data",alpha=0.7)
plt.hist(py.rvs(100),label="model",alpha=0.7)
plt.show()

4.2.1. Usando a regra de Bayes para descobrir um parâmetro

px = norm(loc=-0.2,scale=0.5)
x = px.rvs(200)
px_a =lambda a: norm(loc=a,scale=0.5)

a = 1.0
pa = norm(loc=a,scale=0.5)
score = 0
for i in range(500):
    a = pa.rvs(1000).mean()
    pxa = px_a(a)
    score_ = (pxa.pdf(x).mean()*pa.pdf(a))/px.pdf(x).mean()
    if score_ > score:
        pa = norm(loc=a,scale=0.5)
        score = score_
        
print(a,score)

-0.17513695652847064 0.7979798362224068

previous

3. Entropia e informação mútua

next

5. Decomposição de matrizes