Distribuições de probabilidade
Contents
2. Distribuições de probabilidade¶
Glossário:
Função de distribuição cumulativa (Cumulative distribution function -
CDF): é a funcão \(F: \mathbb{R} \rightarrow \left[ 0,1 \right]\) definida por
onde \(\mathbb{P}\) representa a probabilidade. A função CDF precisa ser sempre crescente e normalizada.
Função de probabilidade (Probability mass function -
PMF): para uma variável discreta \(X\), é dada por \(p = \mathbb{P}(X = x)\) e atende as propriedades: \(p \ge 0 \forall x \in \mathbb{R}\) e \(\sum_{i}p(x_{i}) = 1\).
A relação entre \(F\) e \(p\) é dada por:
Função densidade de probabilidade (Probability density function -
PDF): se \(X\) é uma variável contínua, atende às propriedades: \(p(x) \ge 0 \forall x \in \mathbb{R}\), \(\int_{-\infty}^{+\infty}p(x_{i}) = 1\) e para todo intervalo \(a \le b\)
2.1. Regras da probabilidade¶
Regra da soma: \(p(X) = \sum_{Y}p(X,Y)\) ou \(p(X) = \int{Y}p(X,Y)dy\) para variáveis contínuas.
Regra do produto: \(p(X,Y) = p(Y \vert X)p(X)\).
Teorema de Bayes:
Marginalização:
2.2. Exemplos de Distribuições¶
from scipy.stats import gamma, beta
from scipy.special import gamma as gamma_func
import numpy as np
import matplotlib.pyplot as plt
Função Gamma (não confundir com a distribuição de mesmo nome)
Se \(a\) é um positivo inteiro, então \(\Gamma(a) = (a-1)!\).
2.2.1. Distribuição Gamma¶
PDF:
Parâmetros:
\(k > 0\) shape - número de eventos que desejamos esperar
\(\theta > 0\) scale - \(\frac{1}{\theta}\): taxa de eventos por unidade de tempo
ou ainda
Suporte: \(x \in (0,\infty)\)
Média: \(\mathbb{E}\left[ x \right] = \frac{a}{b}\)
Variância: \(var \left[ x \right] = \frac{a}{b^{2}}\)
Mode: \(moda \left[ x \right] = \frac{a-1}{b} \forall a \ge 1\)
Outras quantidades: \(\mathbb{E}\left[ \ln{x} \right] = \psi(a) - \ln{b},\)
onde \(\psi(a)\) é da função digamma: \(\psi(a) = \frac{d}{da}\ln{\Gamma(a)}\). Para saber mais sobre a função digamma veja aqui.
0.7*0.8,0.4*0.5
(0.5599999999999999, 0.2)
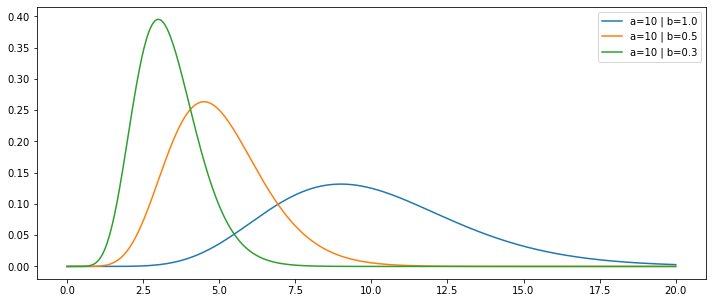
x = np.linspace(0,20,500)
plt.figure(figsize=(12,5))
for i in [1/1,1/2,1/3]:
for j in [10]:
plt.plot(x,gamma(a=j,scale=i).pdf(x),label=f'a={j} | b={i:.1f}')
plt.legend(loc=0)
plt.show()
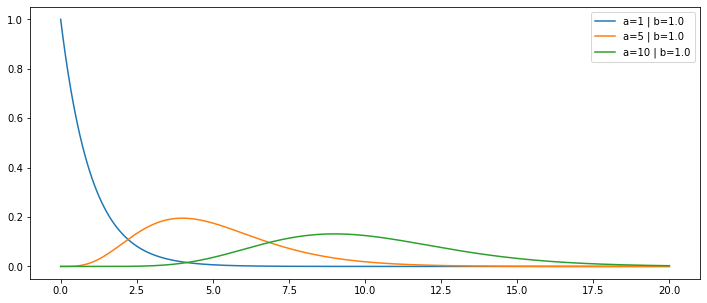
x = np.linspace(0,20,500)
plt.figure(figsize=(12,5))
for i in [1/1]:
for j in [1,5,10]:
plt.plot(x,gamma(a=j,scale=i).pdf(x),label=f'a={j} | b={i:.1f}')
plt.legend(loc=0)
plt.show()
Exemplo de teoria de filas: Você está em uma fila com duas pessoa na sua frente, uma sendo atendida e a outra na sua frente esperando. O tempo médio de espera entre dois serviços independente é de 2 minutos. Isso quer dizer que a taxa de servições por minuto é 0.5/minuto.
Qual é a probabilidade de você esperar mais do que 5 minutos na fila?
\(\theta = 2\) ou \(b = 0.5\) e \(a = k = 2\) (precisamos esperar por dois eventos).
\(\mathbb{P}(X \ge 5) = 1 - \mathbb{P}(X < 5) = 1 - \int_{0}^{5}Gamma(x \vert 2, 0.5)dx\)
p = 1-gamma(a=2,scale=1/0.5).cdf(5)
print(f"Probabilidade de esperar mais do que 5 minutos é {p:.1%}")
Probabilidade de esperar mais do que 5 minutos é 28.7%
2.2.2. Distribuição Beta¶
É uma distribuição sobre uma variável contínua entre \([0,1]\). É normalmente usada para representar a probabilidade de algum evento binário.
PDF:
Parâmetros:
\(a - 1 \): número de sucessos
\(b - 1 \): número de falhas
\(x\) é a probabilidade de sucesso em um experimento de Bernoulli.
Média: \(\mathbb{E}\left[ x \right] = \frac{a}{a+b}\)
Variância: \(var \left[ x \right] = \frac{ab}{(a+b)^{2}(a+b+1)}\)
Mode: \(moda \left[ x \right] = \frac{a-1}{a+b-2}\)
num_suc = 1
num_fail= 7
a = num_suc+1
b = num_fail+1
p = 0.5
(gamma_func(a+b)/(gamma_func(a)*gamma_func(b)))*(p**(a-1))*((1-p)**(b-1))
0.28125
beta(a,b).pdf(0.5)
0.28125000000000006
Qual é a probabilidade de obter mais de 50% de sucesso?
p = 1-beta(a,b).cdf(0.5)
print(f"Probabilidade de obter mais de 50% de sucesso é {p:.2%}")
Probabilidade de obter mais de 50% de sucesso é 1.95%
Qual é a probabilidade de obter menos de 50% de sucesso?
p = beta(a,b).cdf(0.5)
print(f"Probabilidade de obter menos de 50% de sucesso é {p:.2%}")
Probabilidade de obter menos de 50% de sucesso é 98.05%
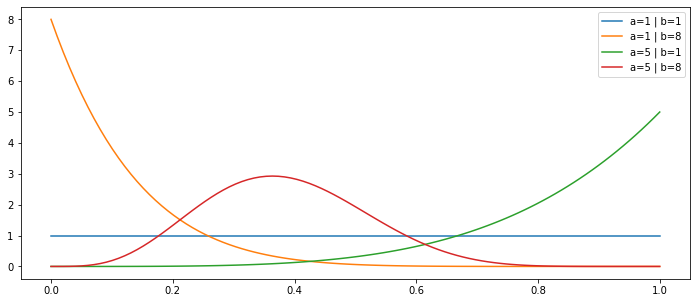
x = np.linspace(0,1,100)
plt.figure(figsize=(12,5))
for i in [1,5]:
for j in [1,8]:
plt.plot(x,beta(a=i,b=j).pdf(x),label=f'a={i} | b={j}')
plt.legend(loc=0)
plt.show()
2.2.3. Distribuição de Poisson ¶
Esta é uma distribuição discreta que expressa a probabilidade de um determinado número de eventos ocorrer em um intervalo fixo (o mais comum é usar para eventos que ocorrem com o tempo), desde que a taxa média de ocorrência seja constante e os eventos sejam independentes do tempo.
Seja \(\lambda\) o número médio eventos por unidade de tempo, podemos escrever a probabilidade de ocorrerem \(k\) eventos em um intervalo \(t\) como:
O valor real positivo \(\lambda t\) é igual ao valor esperado de \(X\) e também igual a variância de \(X\): \(\lambda t = \mathbb{E}(X) = Var(X)\).
import numpy as np
from scipy.stats import poisson
Definimos a distribuição para algum λ:
λ = 5 # nesse caso t=1
poi = poisson(mu=λ)
Podemos fazer uma amostragem dessa distribuição:
x = poi.rvs(size=30)
x
array([ 4, 11, 5, 4, 5, 5, 5, 6, 4, 5, 3, 2, 9, 11, 3, 5, 5,
3, 6, 5, 5, 10, 5, 4, 6, 3, 4, 4, 8, 6])
x.mean(),x.std()**2
(5.366666666666666, 5.098888888888887)
Probabilidade de ocorrer k eventos por unidade de tempo:
k = 3
print(f"Probabilidade de {k} eventos por unidade de tempo é: {poi.pmf(k=k):.2%}")
Probabilidade de 3 eventos por unidade de tempo é: 14.04%
2.2.4. Distribuição Multinomial ¶
Seja um vetor \(\textbf{x}\) de \(K\) dimensões, sendo que cada elemento \(x_{k}\) é uma variável aleatória binária e o vetor obedece o esquema \(1\ de\ K\): um de seus elementos é \(x_{k}=1\) e os demais iguais a \(0\). Exemplo:
\(\textbf{x} = \langle 0,0,1,0,0 \rangle\)
Apenas o elemento \(x_{3}=1\). Note que esse vetor é unitário, \(\sum_{k=1}^{K}x_{k}=1\).
Representamos a probabilidade de \(x_{k}=1\) usando o parâmetro \(\mu_{k}\) e podemos usar o vetor \(\mu=\left( \mu_{1},\mu_{2},...,\mu_{K} \right)\). Assim a distribuição de \(\textbf{x}\) é
Com valor esperado
Note ainda que \(\sum_{k=1}^{K}\mu_{k}=1\) e \(\mu_{k} \in [0,1]\), pois eles representam probabilidades.
import numpy as np
from scipy.stats import multinomial
Methods
-------
pmf(x, n, p)
Probability mass function.
logpmf(x, n, p)
Log of the probability mass function.
rvs(n, p, size=1, random_state=None)
Draw random samples from a multinomial distribution.
entropy(n, p)
Compute the entropy of the multinomial distribution.
cov(n, p)
Compute the covariance matrix of the multinomial distribution.
μ = [0.5,0.3,0.1,0.1]
mult = multinomial(n=1,p=μ)
mult.mean()
array([0.5, 0.3, 0.1, 0.1])
X = mult.rvs(size=10)
X
array([[0, 1, 0, 0],
[1, 0, 0, 0],
[1, 0, 0, 0],
[0, 0, 1, 0],
[1, 0, 0, 0],
[1, 0, 0, 0],
[1, 0, 0, 0],
[1, 0, 0, 0],
[0, 1, 0, 0],
[1, 0, 0, 0]])
Considere um dataset \(\mathcal{D}\) com \(N\) observações independentes \(\textbf{x}_{1},...,\textbf{x}_{N}\). A função de likelihood é
onde \(m_{k} = \sum_{n} x_{nk}\) representa o número de observações em que \(x_{k}=1\).
Dessa maneira, o valor de \(\mu\) que maximiza a likelihood é
que é simplesmente a fração das \(N\) observações em que \(x_{k}=1\). As variáveis \(m_{k}\) estão sujeitas à \(\sum_{k=1}^{K}m_{k}=N\).
A distribuição multinomial é a distribuição conjunta das quantidades \(m_{1},...,m_{K}\) condicionadas ao parâmetro \(\mu\) e ao número total de observações \(N\):
Exemplo: dado um vetor \(\mu = (0.5,0.2,0.3)\), qual é a probabilidade de em 10 observações obtermos \(m_{1}=5,m_{2}=4,m_{3}=1\)?
def normalization_f_multi(m):
N = sum(m)
x = np.array([np.math.factorial(m[i]) for i in range(len(m))])
prod = 1
for i in range(len(m)):
prod *= x[i]
return np.math.factorial(N)/prod
def mult_prod(mu,m):
prod = 1.
for i in range(len(mu)):
prod *= mu[i]**m[i]
return prod
def mult_joint_prob(mu,m):
return normalization_f_multi(m) * mult_prod(mu,m)
mu = [0.5,0.2,0.3]
m = [5,2,3]
mult = multinomial(n=10,p=mu)
normalization_f_multi(m),mult_prod(mu,m)
(2520.0, 3.375e-05)
print("Nossa função:",mult_joint_prob(mu,m))
print("Scipy :",mult.pmf(m))
Nossa função: 0.08505
Scipy : 0.08504999999999999
2.2.5. Distribuição de Dirichlet ¶
A distribuição de Dirichlet pode ser usada para estimar a probabilidade de observarmos o vetor \(\mu\) condicionado a outro parâmetro, o vetor \(\alpha_{k}\), chamado de parâmetro de concentração. A definição geral da distribuição de Dirichlet é
onde \(\alpha_{0} = \sum_{k=1}^{K}\alpha_{k}\) (\(n\) nosso caso coincide com o número total de observações) e \(\Gamma(x)\) é a função gama dada por:
que tem as propriedades: \(\Gamma(x+1)=x\Gamma(x)\); \(\Gamma(1)=1\); e se \(x\) é um número inteiro positivo \(\Gamma(x+1)=x!\).
from scipy.stats import dirichlet
alpha = [1.0,1.0,1.0]
diric = dirichlet(alpha)
diric.mean()
array([0.33333333, 0.33333333, 0.33333333])
x = diric.rvs(size=1000)
x
array([[0.21512095, 0.11100696, 0.67387209],
[0.77522263, 0.16350581, 0.06127156],
[0.20251839, 0.70431946, 0.09316215],
...,
[0.02911277, 0.38263377, 0.58825345],
[0.2982091 , 0.16586772, 0.53592318],
[0.12628688, 0.59331213, 0.28040099]])
x.mean(axis=0)
array([0.33035415, 0.34252115, 0.3271247 ])
diric.pdf(x.mean(axis=0))
2.0