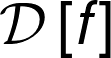Entropia e informação mútua
Contents
3. Entropia e informação mútua¶
3.1. Informação¶
Teoria da informação é uma área muito interessante que nos forneceu métodos para medir coisas relacionadas à ignorância que temos sobre uma hipótese. Sua compreenssão é fundamental para que possamos criar e compreender diversas métricas usadas em machine learning, como a entropia, e também para desenvolver modelo probabilísticos.
Suponha que temos uma variável aleatória \(x\) e estamos interessados na quantidade de informação que obteremos ao medir algum valor de \(x\). Se o evento (resultado de uma medição é \(x\)) é altamente improvável, ao medí-lo obteremos mais informação do que se ele for altamente provável. Se você tem certeza de que algo irá acontecer, não terá nada novo (nenhuma informação extra) quando observar esse evento.
A informação é portanto, dada por uma quantidade \(h(x)\) que é uma função da distribuição de probabilidade \(p(x)\). Se observarmos dois eventos, \(x\) e \(y\), e eles não estiverem relacionados a quantidade total de informação obtida será simplemente a soma da informação dos dois eventos:
Obs: \(\iff\) lê-se “se e somente se”.
Como é costume, descrevemos a informação com o logarítmo da distribuição de probabilidade. Se \(x\) for uma variável discreta podemos usar a base \(2\),
O valor esperado (expectation em inglês, ou esperança se você foi aluno de uma universidade chique) desta quantidade é o que chamamos de entropia da variável \(x\),
Obs: valor esperado é o termo utilizado na Física.
Se a chance de observarmos \(x\) é nula, \(p(x)=0\), não obteremos informação alguma, \(H[x]=0\).
Tomemos um exemplo, suponha que observamos a rolagem de um dado não enviesado de oito faces e queremos transmitir a alguém a informação sobre o valor esperado:
import numpy as np
H = -8*(1/8)*np.log2(1/8)
H
>>> 3.0
Essa quantidade é medida em bits e nesse caso precisamos de um número de pelo menos 3 bits para transmitir essa informação. Caso \(x\) seja contínuo é comum usar o logarítmo natural e a unidade de medida passa a ser nats.
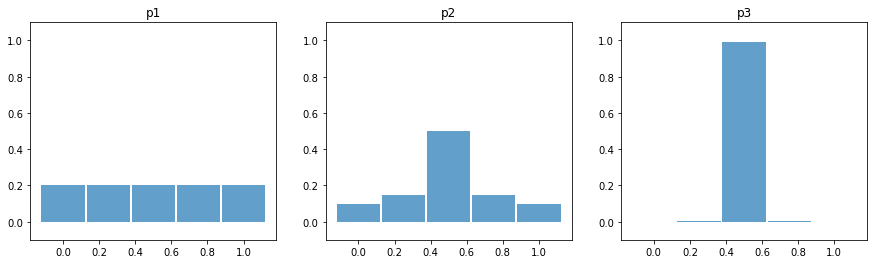
Vejamos um exemplo com três distribuições com a mesma média, mas com diferentes desvios padrões.
p1 = np.array([0.2,0.2,0.2,0.2,0.2])
p2 = np.array([0.1,0.15,0.5,0.15,0.1])
p3 = np.array([0.0,0.005,0.99,0.005,0.0])
import matplotlib.pyplot as plt
plt.figure(figsize=(15,4))
plt.subplot(131)
plt.bar(np.linspace(0,1,5),p1,alpha=0.7,width=0.24)
plt.title("p1")
plt.ylim(-0.1,1.1)
plt.subplot(132)
plt.bar(np.linspace(0,1,5),p2,alpha=0.7,width=0.24)
plt.title("p2")
plt.ylim(-0.1,1.1)
plt.subplot(133)
plt.bar(np.linspace(0,1,5),p3,alpha=0.7,width=0.24)
plt.title("p3")
plt.ylim(-0.1,1.1)
plt.show()
Definimos uma função para calcular a entropia:
def H(p):
return np.sum([-val*np.log(val) if val > 0 else 0 for val in p])
H(p1),H(p2),H(p3)
>>> (1.6094379124341005, 1.376226604344546, 0.06293300616044681)
A distribuição mais estreita tem menor entropia. Isso ocorre pois a incerteza que temos sobre seu valor esperado é menor. Novamente, se alguma distribuição é \( p(x_{i})=1 \) o resto todo será \(p(x_{j \ne i})=0\), ou seja, incerteza nula e informação \(H(x_{i})=0\).
3.2. Entropia diferencial ¶
Podemos também usar uma distribuição \(p(x)\) contínua e assim a soma discreta se torna uma integral. Neste caso é comum chamar a entropia de entropia diferencial:
Algo que acho muito interessante é responder a pergunta Qual é a distribuição de probabilidade que maximiza a entropia?
A distribuição Gaussiana é aquela que maximiza a entropia diferencial (isso faz sentido, pois é a distribuição favorita da natureza):
Este resultado concorda com o exemplo visto anteriormente, a entropia aumenta conforme a distribuição se torna mais larga, ou seja, \(\sigma^{2}\) aumenta. No fim dessa lição há mais detalhes sobre esse desenvolvimento.
3.3. Entropia condicional ¶
Mudamos agora para o caso em que temos uma distribuição conjunta, digamos \(p(x,y)\) e temos uma observação de \(x\). Como as duas variáveis estão ligadas de alguma forma é possível calcular a quantidade de informação necessária para especificar a observação correspondente de \(y\) com \(- \ln p(y\vert x)\). Assim, o valor esperado de informação adicional para espeficicar \(y\), chamada de entropia condicional de \(y\) dado \(x\) é:
Usando \(p(y\vert x) = \frac{p(y,x)}{p(x)}\) temos:
3.4. Divergência de Kullback-Leibler ¶
A classe de métricas conhecidas como divergências são usadas para medir distância entre distribuições de probabilidade, uma das mais famosas é a divergência de Kullback-Liebler (divergência KL ou apenas \(D_{KL}\)). Vamos ver como construí-la usando os conceitos de entropia.
Suponha que temos uma distribuição desconhecida \(p(x)\) e nós estamos usando outra distribuição \(q(x)\) para modelar a anterior, ou seja, queremos que \(q\) igual a \(p\). Podemos calcular a quantidade de informação adicional necessária para especificar \(x \sim p(x)\) ao observar \(x \sim q(x)\):
Essa entropia relativa entre as duas distribuição é a Divergência KL e é a medida de dissimilaridade entre duas distribuições. Devemos notar que ela é antissimétrica,
Para aproximar \(q(x)\) de \(p(x)\) podemos obvservar \(x \sim p(x)\) um número finito de vezes, \(N\), usar \(q\) como uma função paramétrica, \(q(x \vert \theta)\) e usar o valor esperado de \(D_{KL}(p \vert \vert q)\) como função de perda dentro da estratégia de otimização escolhida.
O valor esperado de uma função da variável aleatória \(x\), \(f(x)\), é dada por \(\mathbb{E}[f] = \int p(x) f(x)dx\) e para um número finito de observações \(N\) e integral se torna uma soma finita:
Fazemos isso para obter o valor esperado de \(D_{KL}\):
O primeiro termo é o negativo do log da verossimilhança (negative log likelihood) da distribuição \(q(x\vert \theta)\) usando um conjunto de parâmetros \(\theta\). É por esse motivo que costuma-se dizer minimizar a \(D_{KL}\) é equivalente a maximizar a função de verossimilhança.
Como um exemplo podemos supor as duas distribuições normais:
para encontrar \(D_{KL} \left( p \vert \vert q \right)\) (o desenvolvimento está no final do post):
onde \((\langle x \rangle -m)^{2} -\langle x \rangle^{2} = -2 \langle x \rangle m + m^{2}\). Se as variâncias \(\sigma^{2}\) e \(s^{2}\) forem iguais os três primeiros termos se anulam, já se as médias forem iguais o último termo se anula. Isso pode ser usado para saber o quanto uma distribuição se afasta da normal “pela direita” ou “pela esquerda”, devido a propriedade de antissimetria.
3.4.1. f-Divergence ¶
Como dito antes, a divergência KL é a mais famosa de uma grande família conhecida como \(f\)-divergências, definidas de maneira mais geral como:
onde \(f\) é um parâmetro contínuo, \(-\infty \le f \le + \infty\). Alguns casos especiais são:
e a distância de Hellinger:
Como as distribuições de probabilidade tem suporte compacto \(D_{f}(p \vert \vert q) \ge 0\), novamente, a divergência é zero se e somente se \(p(x) = q(x)\).
3.5. Informação mútua ¶
Para um distribuição conjunta \(p(y,x)\) a \(D_{KL}\) pode ser usada para quantificar o quão próximas duas variáveis estão de serem independentes, ou seja, \(p(y,x) = p(y)p(x)\). Isso é chamado de informação mútua entre \(x\) e \(y\):
\(I[y,x] \ge 0\) e \(I[y,x] = 0 \iff\) \(x\) e \(y\) são independentes.
Por fim a informação mútua pode ser escrita em termos da entropia condicional:
3.6. Medindo entropia¶
3.6.1. A distribuição que maximiza a entropia ¶
Como discutido anteriormente, vamos responder: Qual é a distribuição de probabilidade que maximiza a entropia?
Podemos fazer isso usando a técnica de multiplicadores de Lagrange restringindo o primeiro e segundo momentos de \(p(x)\) juntamente com sua normalização:
Ao fazer a derivada variacional ir a zero encontraremos a solução \(p(x) = \exp{(-1 + \lambda_{1} + \lambda_{2} x + \lambda_{3} (x - \mu)^{2})}\). Ao substituir a solução nas equações acima encontraremos:
3.6.2. \(D_{KL} \left( p(x) \vert \vert q(x) \right)\) entre duas distribuições Normais ¶
É possível encontrar uma forma fechada para a divergência \(KL\) entre duas distribuições Normais. Vejamos a seguir o desenvolvimento para isso.
Objetivo: Calcular \(D_{KL} \left( p(x) \vert \vert q(x) \right)\) para \(p(x)=\mathcal{N}(x\vert \mu, \sigma^{2})\) e \(q(x)=\mathcal{N}(x\vert m, s^{2})\)
\(D_{KL} \left( p \vert \vert q \right) = -\int p(x) \ln{\frac{q(x)}{p(x)}}dx\)
\(D_{KL} \left( p \vert \vert q \right) = -\int p(x) \ln{q(x)}dx + \int p(x) \ln{p(x)}dx\)
\(D_{KL} \left( p \vert \vert q \right) = \frac{1}{2}\int p(x) \ln{2 \pi s^{2}}dx + \frac{1}{2s^{2}}\int p(x)(x-m)^{2}dx - \frac{1}{2}(1+\ln{2 \pi \sigma^{2}})\)
\(D_{KL} \left( p \vert \vert q \right) = \frac{1}{2}\ln{2 \pi s^{2}} - \frac{1}{2}(1+\ln{2 \pi \sigma^{2}})+ \frac{1}{2s^{2}}(\langle x \rangle^{2} -2m \langle x \rangle + m^{2})\)
\(D_{KL} \left( p \vert \vert q \right) = \frac{1}{2} \ln{\frac{s^{2}}{\sigma^{2}}} - \frac{1}{2} + \frac{\sigma^{2}+(\mu - m)^{2}}{2s^{2}}\)
\(D_{KL} \left( p \vert \vert q \right) = \ln{\frac{s}{\sigma}} - \frac{1}{2} + \frac{\sigma^{2}+(\mu - m)^{2}}{2s^{2}}\)
3.6.3. Pointwise Mutual Information ¶
A PMI é uma medida de associação entre a ocorrência de dois eventos. No nosso caso os eventos são a ocorrência ou não de tokens pertencentes ao corpus. Sejam duas variáveis aleatórias discretas \(x \sim X\) e \(y \sim Y\). A PMI é a distância, no espaço de log, entre as probabilidades conjunta e disjunta destas duas variáveis, em outras palavras, ela mede o quão distante os dois eventos estão de serem independentes. A PMI é máxima se o pair \(x,y\) sempre ocorre junto.
\(PMI(x,y) \equiv \log{\frac{p(x,y)}{p(x)p(y)}}\)
3.6.4. Likelihood ratio ¶
Dado que estamos interessados em identificar uma collocation (bi-grama) composta pelos tokens \(w^1 w^2\), podemos ter duas hipóteses:
\(H_{1}\)(Independência): \(P(w^{2} \vert w^{1}) = p = P(w^{2} \vert \neg w^{1})\)
\(H_{2}\)(Dependência): \(P(w^{2} \vert w^{1}) = p_{1} \neq p_{2} = P(w^{2} \vert \neg w^{1})\)
Sejam \(c_{1}\) as ocorrências de \(w^{1}\),\(c_{2}\) de \(w^{2}\), \(c_{12}\) de \(w^{1}w^{2}\) e \(N\) o número total de observações. Temos:
\(p=\frac{c_{2}}{N},\ p_{1}=\frac{c_{12}}{c_{1}},\ p_{2}=\frac{c_{2}-c_{12}}{N-c_{1}}\)
A ocorrência de um evento deste tipo é dada por uma distribuição binomial (probabilidade de conseguir \(k\) sucessos em \(n\) experimentos de Bernoulli, sendo que a chance de sucesso em cada é \(p\)):
\(B(k;n,p) = \frac{n!}{k!(n-k)!} p^{k}(1-p)^{n-k}\)
Assim a likelihood das hipóteses 1 e 2 são:
\(L(H_{1})=B(c_{12};c_{1},p)B(c_{2}-c_{12};N-c_{1},p)\)
\(L(H_{2})=B(c_{12};c_{1},p_{1})B(c_{2}-c_{12};N-c_{1},p_{2})\)
No fim das contas, a razão entre as likelihoods é outra maneira de medir o quanto a ocorrência entre os dois tokens estão de ser independentes:
\(\lambda=\frac{L(H_{1})}{L(H_{2})}\).
Um valor \(\lambda=1\) significa que as duas hipóteses são igualmente prováveis, já \(\lambda < 1\) indica que a hipótese 2 (dependência) é a mais provável.