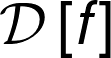Variational AutoEncoder
12. Variational AutoEncoder¶
Variational AutoEncoders or VAE are a class of generative models based on latent variables. Suppose we have our multidimensional data \(X\) and we want to build a model from which we can sample data at least similar to \(X\). We will make that with a multidimensional latent variable \(Z\) to create a map \(f:Z \to X\).
We need to model \(p(X) = \int p(X \vert Z)dZ\), where \(p(X,Z) = p(X \vert Z)p(Z)\).
The ideia of VAE is to infer \(p(Z)\), but at first \(p(Z \vert X)\) is unknown. To deal with that let us use a method called Variational Inference (VI). It is very popular together with Markov Chain Monte Carlo (MCMC) methods.
We treat this as an optimization problem, we model \(p(Z \vert X)\) using some distribution and minimize the Kullback-Liebler (KL) divergence between our chosen distribution, let us call it \(q(Z \vert X)\), and \(p(Z \vert X)\). We have
and we use Bayes Theorem treating \(p(Z \vert X)\) as a posterior: \(p(Z \vert X) = \frac{p(X \vert Z)p(Z)}{p(X)}\) rewriting the KL divergence
Since the expectation is over \(Z\) the term \(\log{p(X)}\) is constant and can be factored out. Looking closely we see another KL divergence inside the expectation
\(\mathbb{E}_{Z} \left[\log{q(Z \vert X)} - \log{p(Z)} \right] = KL \left[q(Z \vert X)\vert \vert p(Z) \right]\). Rearranging the equation we have the VAE objective function.
Let us see the meaning of all these distributions:
\(q(Z \vert X)\) is a function which projects \(X\) into latent space.
\(p(X \vert Z)\) is a function which projects \(Z\) into features space.
It is common to say that \(q(Z \vert X)\) encodes the information of \(X\) as \(Z\) and \(p(X \vert Z)\) do the opposite, decodes \(Z\) back to \(X\). In the ideal case we want the following diagram to commute
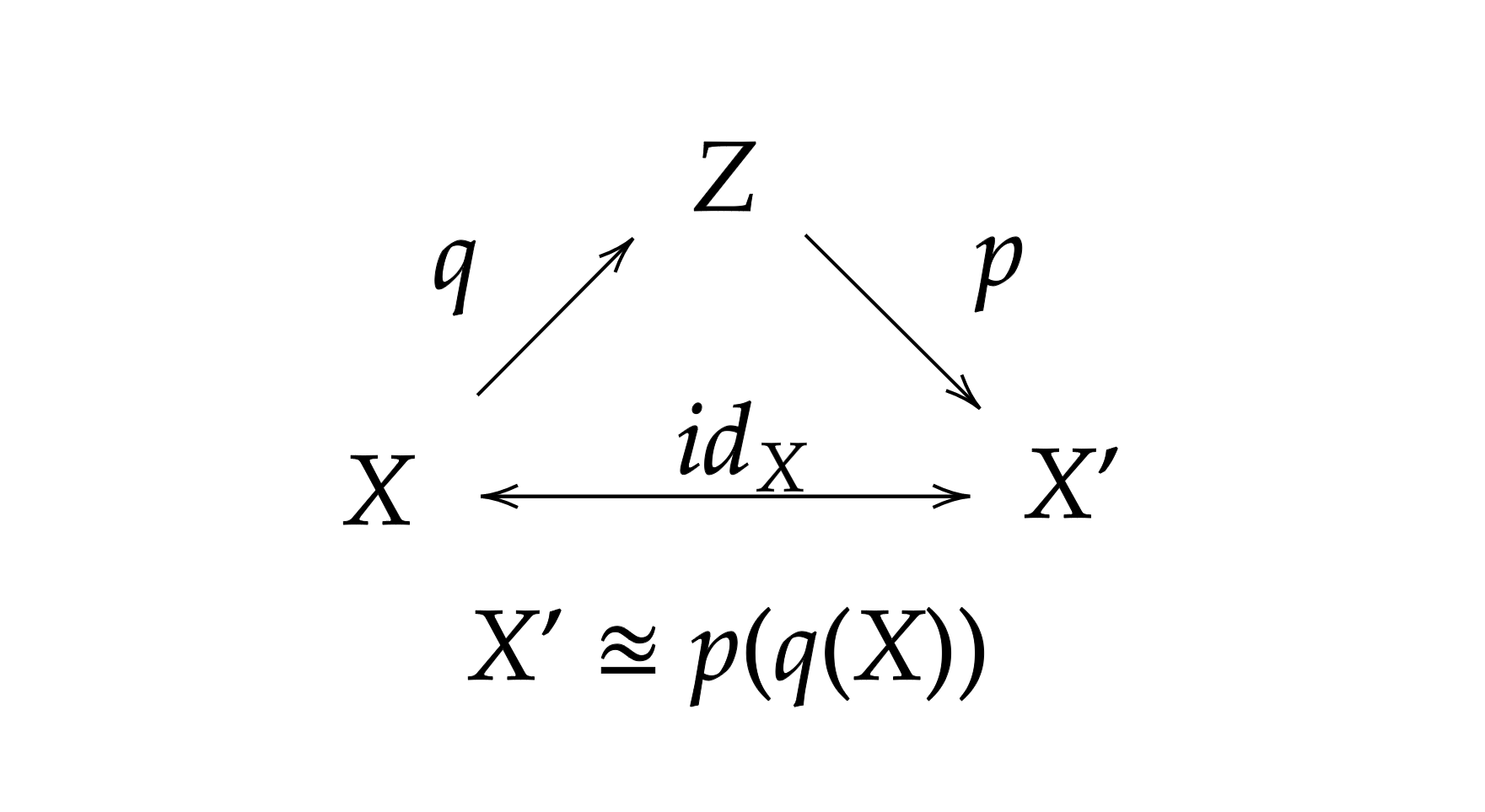
On summary, looking at \(\mathcal{L} = \log{p(X)} - KL \left[q(Z \vert X)\vert \vert p(Z \vert X) \right]\) we want to model \(\log{p(X)}\) setting an error \(KL \left[q(Z \vert X)\vert \vert p(Z \vert X) \right]\), i.e., the VAE tries to find a lower bound to \(\log{p(X)}\), which is intractable.
The model can be found maximizing \(\log{p(X \vert Z)}\) and minimizing the difference between \(q(Z \vert X)\) and \(p(Z)\),
Remember that maximizing \(\mathbb{E} \left[\log{p(X \vert Z)} \right]\) is an estimation by maximum likelihood.
There is only one question left. What kind of distribution should we use for \(p(Z)\)? We can try a something simple like a normal distribution with zero mean and variance one, \(\mathcal{N}(0,1)\). Given \(KL \left[q(Z \vert X) \vert \vert p(Z) \right]\), we want \(q(Z \vert X)\) to be as near as possible of \(\mathcal{N}(0,1)\). The good part of the choice is that we have a closed form for the KL divergence. Let us represent the mean by \(\mu(X)\) and the variance by \(\Sigma(X)\). The KL divergence is (we computed this in the Information Theory post)
where \(k\) is the Gaussian dimension. You will see that in practice it is stable if we use \(\Sigma(X)\) as \(\log{\Sigma(X)}\) and finally we have