Gradiente descendente
Contents
6. Gradiente descendente¶
Dada uma função \(f(x)\), queremos aproximá-la usando uma função com parâmetros \(w\), digamos \(g(x;w)\). Queremos saber quais são os valores dos parâmetros que minimizam alguma forma de diferença entre as duas funções.
import numpy as np
import matplotlib.pyplot as plt
def get_data_and_functions():
sign = lambda :2*np.random.binomial(n=1,p=0.5)-1
param = lambda a,b: np.random.normal(a,b)
x1 = np.linspace(-2,2,20)
x2 = x1**2
f = lambda x1,x2: sign()*param(1,0.2)*x1 +sign()*param(2,0.5)*x2
g = lambda x1,x2: sign()*param(1,0.2)*x1 +sign()*param(2,0.5)*x2 +2.5*x1**3 + 0.5*x1**4
return x1,x2,f,g
x1,x2,f,g = get_data_and_functions()
y = f(x1,x2)
y = f(x1,x2)
plt.figure(figsize=(20,6))
plt.subplot(131)
plt.ylabel("y")
plt.xlabel("x1")
plt.plot(x1,y)
plt.grid(True)
plt.subplot(132)
plt.ylabel("y")
plt.xlabel("x2")
plt.plot(x2,y)
plt.grid(True)
plt.subplot(133)
plt.ylabel("x1")
plt.xlabel("x2")
plt.plot(x2,x1)
plt.grid(True)
plt.show()
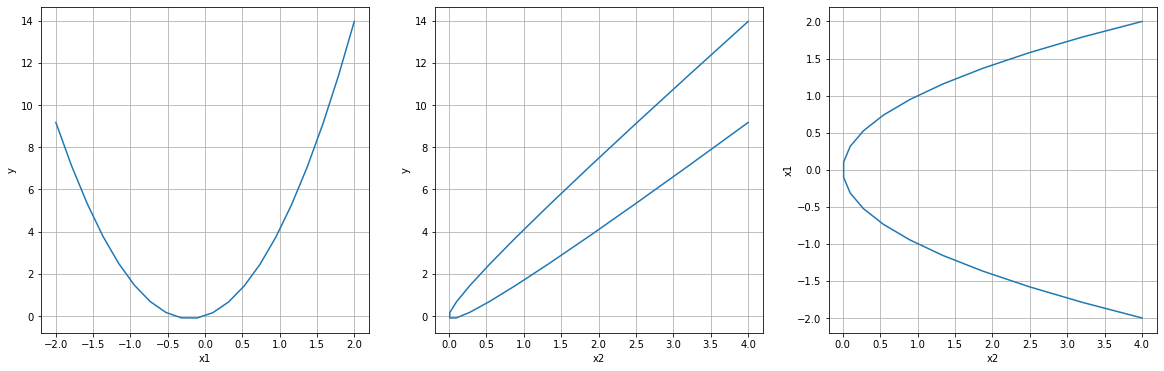
# prediction
compute_prediction = lambda w,x1,x2: w @ np.array([x1,x2])
# pesos iniciais
w = np.array([1.0,1.0])
p = compute_prediction(w,x1,x2)
squared_error = lambda y,p: np.mean((y-p)**2)
es = squared_error(y,p)
def plot_y_vs_p_error():
print(f"Squared error: {es:.4f}")
plt.figure(figsize=(12,4))
plt.subplot(121)
plt.ylabel("y,p")
plt.xlabel("x1")
plt.plot(x1,y,label="y")
plt.plot(x1,p,label="p")
plt.legend(loc=0)
plt.subplot(122)
plt.ylabel("y,p")
plt.xlabel("x2")
plt.plot(x2,y,label="y")
plt.plot(x2,p,label="p")
plt.legend(loc=0)
plt.show()
plot_y_vs_p_error()
>>> Squared error: 4.0259
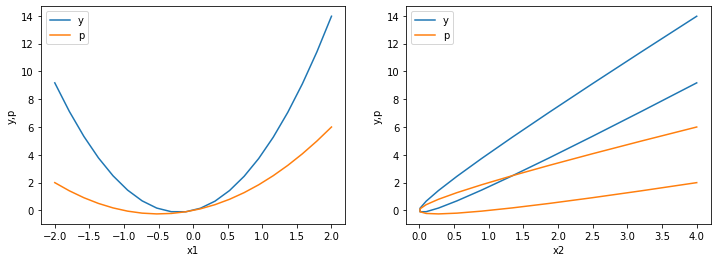
Parece que nossa suposição para o formato de \(g(x,w)\) foi correta. Podemos fazer um grid search pelos parâmetros \(w\) para encontrar valores que minimizam o erro.
def compute_results():
results = {"p":[],
"es":[],
"w1":[],
"w2":[],
"wi_optm":[],
"min_error":np.infty}
for w1 in np.linspace(-5,5,20):
for w2 in np.linspace(-5,5,20):
w = np.array([w1,w2])
p = compute_prediction(w,x1,x2)
es = squared_error(y,p)
if es < results["min_error"]:
results["min_error"] = es
results["wi_optm"] = [w1,w2]
results["w1"].append(w1)
results["w2"].append(w2)
results["p"].append(p)
results["es"].append(es)
return results
###########################
results = compute_results()
###########################
print(f"Optimal parameters: w1={results['wi_optm'][0]}, w2={results['wi_optm'][1]}")
print(f"Minimum error: {results['min_error']:.4f}")
plt.figure(figsize=(18,4))
plt.subplot(121)
plt.plot(results["w1"],results["es"],'.',label="w2=0.0")
plt.hlines(y=results["min_error"],xmin=-5,xmax=5,linestyles='dashed',color='black',label="min_error")
plt.ylabel("Error")
plt.xlabel(r"$w_{1}$")
plt.grid(True)
plt.subplot(122)
plt.plot(results["w2"],results["es"],'.',label="w1=0.0")
plt.hlines(y=results["min_error"],xmin=-5,xmax=5,linestyles='dashed',color='black',label="min_error")
plt.ylabel("Error")
plt.xlabel(r"$w_{2}$")
plt.grid(True)
plt.show()
>>> Optimal parameters: w1=1.3157894736842106, w2=2.894736842105263
>>> Minimum error: 0.0207
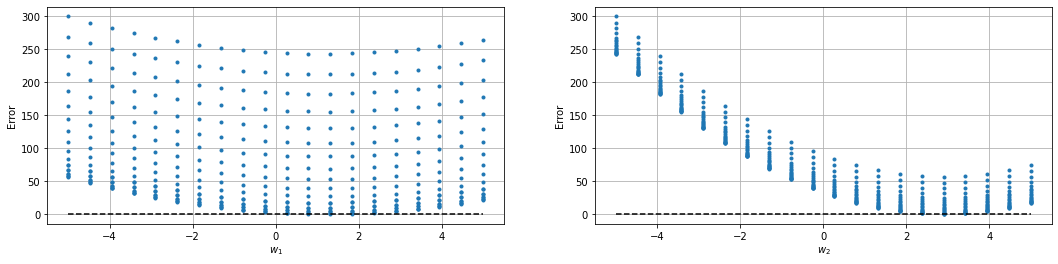
Agora vamos comparar a curva verdadeira com a nossa melhor curva:
w = np.array(results["wi_optm"])
p = compute_prediction(w,x1,x2)
squared_error = lambda y,p: np.mean((y-p)**2)
es = squared_error(y,p)
plot_y_vs_p_error()
>>> Squared error: 0.0207
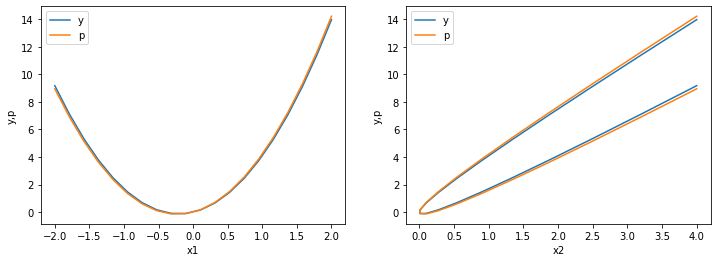
Muito bom! Trabalho feito e isso é tudo que você poderia aprender sobre otimização, certo?
insira sua risadinha favorita
Esse caso que usamos é muito simples, pois fomos capazes de:
inferir um formato para \(g(x,w)\);
buscar por um espaço de parâmetros pequeno;
escolher uma métrica de erro adequada.
Isso ocorre por vários motivos:
não há ruído nos dados;
a verdadeira forma de \(f(x)\) é bem comportada;
existe apenas um mínimo global na função de erro;
temos todas as variáveis que formam \(f(x)\);
o espaço de features é de baixa dimensão.
Então o que podemos fazer quando não temos essas condições?
O algoritmo mais bem sucedido, pesquisado e popular até hoje para fazer otimização, mesmo não sendo perfeito, é o gradiente descendente/ascendente.
Observe o gráfico abaixo:
def compute_es_from_w(X,Y):
es_value = lambda w1,w2,x1,x2: squared_error(y,compute_prediction(np.array([w1,w2]),x1,x2))
es_matrix = []
for x_,y_ in zip(X,Y):
for w1_,w2_ in zip(x_,y_):
es_matrix.append(es_value(w1_,w2_,x1,x2))
return np.array(es_matrix).reshape(20,20)
from matplotlib import cm
fig, ax = plt.subplots(subplot_kw={"projection": "3d"})
fig.set_size_inches((12,7))
X, Y = np.meshgrid(np.linspace(-4,8,20),np.linspace(-4,8,20))
Z = compute_es_from_w(Y,X)
surf = ax.plot_surface(X, Y, Z, cmap=cm.coolwarm,
linewidth=0, antialiased=False)
ax.set_xlabel('w2')
ax.set_ylabel('w1')
ax.set_zlabel('Error')
fig.colorbar(surf, shrink=0.9, aspect=5)
ax.view_init(30, 65) # (rotação de z, rotação de x,y)
plt.show()
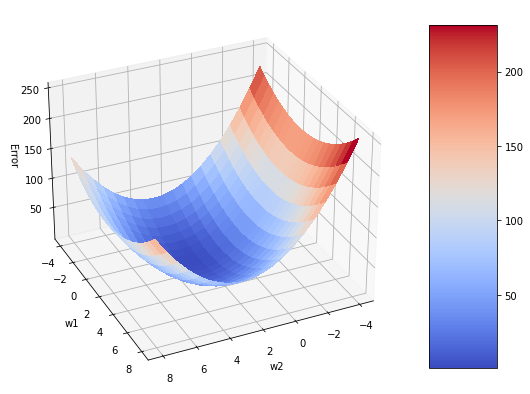
Dado um ponto na superfície de erro, o GD nos permite olhar para o redor deste ponto e verificar a direção para a qual o erro diminui mais. Assim é possível atualizar os parâmetros para este novo ponto no espaço.
6.1. A derivada ou reta tangente¶
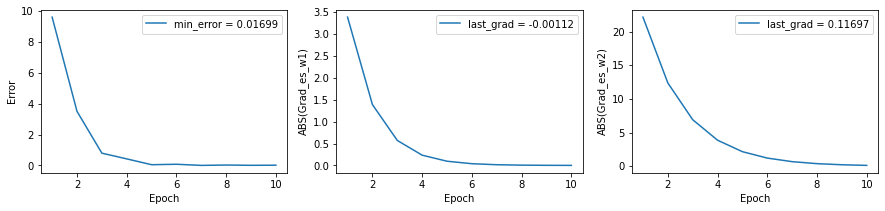
Vamos procurar por um bom valor de w1, mantendo w2 fixo usando o GD:
\(\epsilon \equiv \) step_size
es_value = lambda w1,w2,x1,x2: squared_error(y,compute_prediction(np.array([w1,w2]),x1,x2))
w1,w2 = [1.0,1.0]
step_size_w1 = 0.1
lr= 0.2
epochs=10
for i in range(epochs):
grad_es_w1 = (es_value(w1+step_size_w1,w2,x1,x2)-es_value(w1,w2,x1,x2))/step_size_w1
w1 = w1 - lr * np.sign(grad_es_w1) * abs(grad_es_w1)
print(f"w1 = {w1:.3f}, Grad = {grad_es_w1:.5f}, Error = {es_value(w1,w2,x1,x2):.3f}")
>>> w1 = 1.087, Grad = -0.43450, Error = 13.972
>>> w1 = 1.123, Grad = -0.17837, Error = 13.963
>>> w1 = 1.137, Grad = -0.07323, Error = 13.960
>>> w1 = 1.143, Grad = -0.03006, Error = 13.959
>>> w1 = 1.146, Grad = -0.01234, Error = 13.958
>>> w1 = 1.147, Grad = -0.00507, Error = 13.958
>>> w1 = 1.147, Grad = -0.00208, Error = 13.958
>>> w1 = 1.147, Grad = -0.00085, Error = 13.958
>>> w1 = 1.147, Grad = -0.00035, Error = 13.958
>>> w1 = 1.147, Grad = -0.00014, Error = 13.958
def optimizer(w1,w2,lr,step_size_w1,step_size_w2,epochs):
error = []
grads = [[],[]]
for i in range(epochs):
grad_es_w1 = (es_value(w1+step_size_w1,w2,x1,x2)-es_value(w1,w2,x1,x2))/step_size_w1
grad_es_w2 = (es_value(w1,w2+step_size_w2,x1,x2)-es_value(w1,w2,x1,x2))/step_size_w2
w1 = w1 - lr * np.sign(grad_es_w1) * abs(grad_es_w1)
w2 = w2 - lr * np.sign(grad_es_w2) * abs(grad_es_w2)
error.append(es_value(w1,w2,x1,x2))
grads[0].append(grad_es_w1)
grads[1].append(grad_es_w2)
return w1,w2,error,grads
#######################
epochs = 10
w1,w2,error,grads = optimizer(w1=0.0,w2=0.0,lr=0.2,step_size_w1=0.1,step_size_w2=0.1,epochs=epochs)
#######################
plt.figure(figsize=(15,3))
plt.subplot(131)
plt.plot(range(1,epochs+1),error,label=f"min_error = {error[-1]:.5f}")
plt.xlabel("Epoch")
plt.ylabel("Error")
plt.legend(loc=0)
plt.subplot(132)
plt.plot(range(1,epochs+1),np.abs(grads[0]),label=f"last_grad = {grads[0][-1]:.5f}")
plt.xlabel("Epoch")
plt.ylabel("ABS(Grad_es_w1)")
plt.legend(loc=0)
plt.subplot(133)
plt.plot(range(1,epochs+1),np.abs(grads[1]),label=f"last_grad = {grads[1][-1]:.5f}")
plt.xlabel("Epoch")
plt.ylabel("ABS(Grad_es_w2)")
plt.legend(loc=0)
plt.show()
#######################
epochs = 10
w1,w2,error,grads = optimizer(w1=-10.0,w2=10.0,lr=0.2,step_size_w1=0.1,step_size_w2=0.05,epochs=epochs)
#######################
plt.figure(figsize=(15,3))
plt.subplot(131)
plt.plot(range(1,epochs+1),error,label=f"min_error = {error[-1]:.5f}")
plt.xlabel("Epoch")
plt.ylabel("Error")
plt.legend(loc=0)
plt.subplot(132)
plt.plot(range(1,epochs+1),np.abs(grads[0]),label=f"last_grad = {grads[0][-1]:.5f}")
plt.xlabel("Epoch")
plt.ylabel("ABS(Grad_es_w1)")
plt.legend(loc=0)
plt.subplot(133)
plt.plot(range(1,epochs+1),np.abs(grads[1]),label=f"last_grad = {grads[1][-1]:.5f}")
plt.xlabel("Epoch")
plt.ylabel("ABS(Grad_es_w2)")
plt.legend(loc=0)
plt.show()
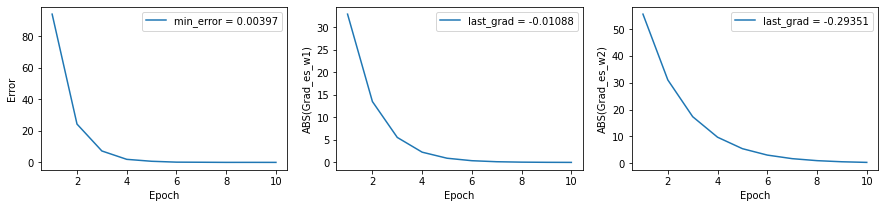
w = np.array([w1,w2])
p = compute_prediction(w,x1,x2)
squared_error = lambda y,p: np.mean((y-p)**2)
es = squared_error(y,p)
plot_y_vs_p_error()
>>> Squared error: 0.0040
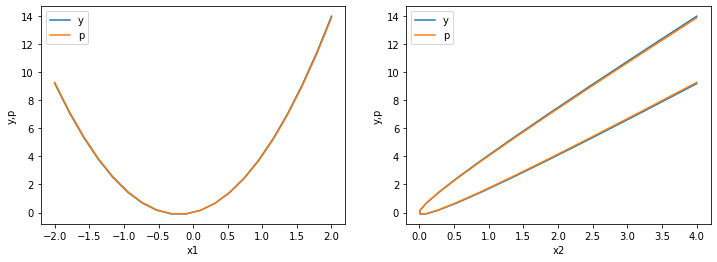
Vamos melhorar o critério de parada do algoritmo
def improved_optimizer(w1,w2,lr,step_size_w1,step_size_w2,epochs,grad_stop_criterion):
error = []
grads = [[],[]]
for i in range(epochs):
grad_es_w1 = (es_value(w1+step_size_w1,w2,x1,x2)-es_value(w1,w2,x1,x2))/step_size_w1
grad_es_w2 = (es_value(w1,w2+step_size_w2,x1,x2)-es_value(w1,w2,x1,x2))/step_size_w2
w1 = w1 - lr * np.sign(grad_es_w1) * abs(grad_es_w1)
w2 = w2 - lr * np.sign(grad_es_w2) * abs(grad_es_w2)
error.append(es_value(w1,w2,x1,x2))
grads[0].append(grad_es_w1)
grads[1].append(grad_es_w2)
if max(abs(grad_es_w1),abs(grad_es_w2)) <= grad_stop_criterion:
break
return w1,w2,error,grads
#######################
epochs = 500
w1,w2,error,grads = improved_optimizer(w1=-10.0,w2=10.0,lr=0.1,step_size_w1=0.01,step_size_w2=0.01,epochs=epochs,grad_stop_criterion=1e-4)
#######################
plt.figure(figsize=(15,3))
plt.subplot(131)
plt.plot(range(1,len(grads[0])+1),error,label=f"min_error = {error[-1]:.5f}")
plt.xlabel("Epoch")
plt.ylabel("Error")
plt.legend(loc=0)
plt.subplot(132)
plt.plot(range(1,len(grads[0])+1),np.abs(grads[0]),label=f"last_grad = {grads[0][-1]:.5f}")
plt.xlabel("Epoch")
plt.ylabel("ABS(Grad_es_w1)")
plt.legend(loc=0)
plt.subplot(133)
plt.plot(range(1,len(grads[0])+1),np.abs(grads[1]),label=f"last_grad = {grads[1][-1]:.5f}")
plt.xlabel("Epoch")
plt.ylabel("ABS(Grad_es_w2)")
plt.legend(loc=0)
plt.show()
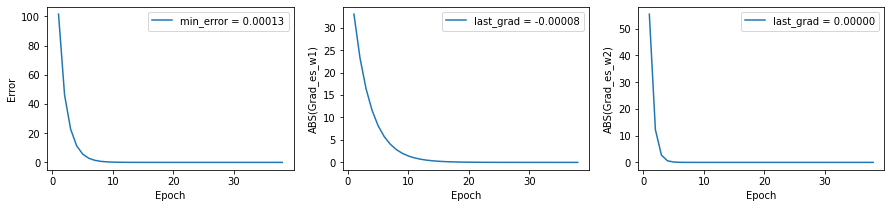
w = np.array([w1,w2])
p = compute_prediction(w,x1,x2)
squared_error = lambda y,p: np.mean((y-p)**2)
es = squared_error(y,p)
plot_y_vs_p_error()
>>> Squared error: 0.0001
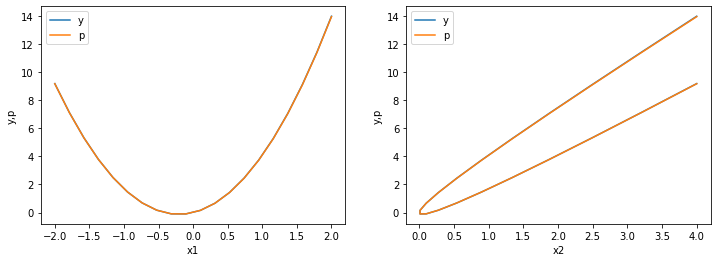
Agora podemos tentar com uma função um pouco mais complicada
y = g(x1,x2)
epochs = 5000
w1,w2,error,grads = improved_optimizer(w1=0.0,w2=0.0,lr=0.01,step_size_w1=0.01,step_size_w2=0.01,epochs=epochs,grad_stop_criterion=1e-6)
plt.figure(figsize=(15,3))
plt.subplot(131)
plt.plot(range(1,len(grads[0])+1),error,label=f"min_error = {error[-1]:.5f}")
plt.xlabel("Epoch")
plt.ylabel("Error")
plt.legend(loc=0)
plt.subplot(132)
plt.plot(range(1,len(grads[0])+1),np.abs(grads[0]),label=f"last_grad = {grads[0][-1]:.5f}")
plt.xlabel("Epoch")
plt.ylabel("ABS(Grad_es_w1)")
plt.legend(loc=0)
plt.subplot(133)
plt.plot(range(1,len(grads[0])+1),np.abs(grads[1]),label=f"last_grad = {grads[1][-1]:.5f}")
plt.xlabel("Epoch")
plt.ylabel("ABS(Grad_es_w2)")
plt.legend(loc=0)
plt.show()
w = np.array([w1,w2])
p = compute_prediction(w,x1,x2)
plot_y_vs_p_error()
>>> Squared error: 0.0001
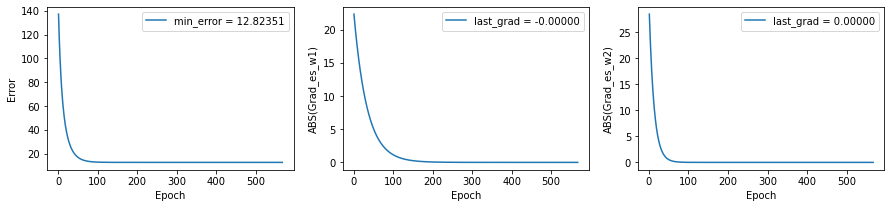
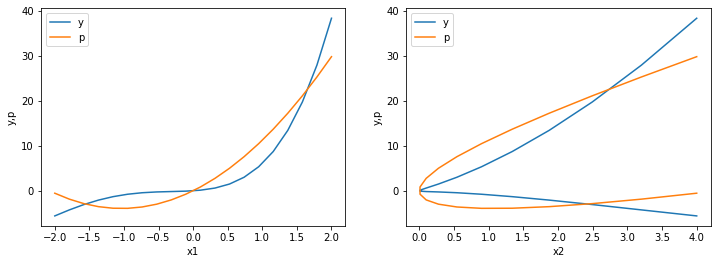
Uma falha miserável, não é mesmo?
Só o GD não é suficiente…
6.2. Mais dimensões e mais derivadas¶
A função de erro que estávamos usando até agora é um campo escalar, ou seja, mapeia cada ponto do espaço de parâmetros para um escalar, \(\mathcal{L}: \mathbb{R}^{m} \rightarrow \mathbb{R}^{1}\).
Já o gradiente é um operador vetorial. Quando aplicado a um campo escalar retorna um campo vetorial, \(\vec{\nabla} [\mathcal{L}]: \mathbb{R}^{m} \rightarrow \mathbb{R}^{n}\).
No nosso caso, sendo \(\mathcal{L} \equiv squared\_error(w_{1},w_{2})\) temos:
Ou ainda:
Note que o índice em cima significa vetor coluna, enquanto o contrário é vetor linha.
Assim, o gradiente do erro é um campo vetorial, para cada ponto do espaço de parâmetros nos informa a intensidade e direção para da máxima variação do erro.
6.2.1. Jacobiano¶
Seja \(\mathcal{F}(w)\) uma campo vetorial \(\mathcal{F}: \mathbb{R}^{m} \rightarrow \mathbb{R}^{n}\), o Jacobiano é a matriz \(J \in \mathbb{R}^{n \times m}\) de \(\mathcal{F}(w)\), tal que
Como o gradiente é um campo vetorial, o Jacobiano dele é:
Explicitamente para o nosso caso:
Perceba que se abrirmos os gradientes, teremos derivadas segundas, algumas cruzadas:
Essa matriz (Jacobiano de um gradiente) é chamada de Hessian do campo escalar \(\mathcal{L}\):
Caso você fique em dúvida em relação a ordem dos índices \(i\) e \(j\), a matriz \(H\) é simétrica, ou seja, \(H_{j}^{\ i} = H^{i}_{\ j}\) desde que as segundas derivadas existam e sejam contínuas.
Eu sei que você está desconfiado pensando para que isso tudo serve.
Acontece que se a primeira derivada nos diz a direção de variação de \(\mathcal{L}\), a segunda derivada diz a direção de variação da direção de variação de \(\mathcal{L}\), legal, né? :)
Em outras palavras, nos diz qual é a curvatura local. Isso pode ser usado para saber se o gradiente está aumentando ou diminuindo.
O gradiente pode ainda estar diminuindo conforme nosso algoritmo itera, mas pode ser que ele já esteja “perdendo força”. Podemos usar a informação do Hessian como um critério de parada do algoritmo.
Suponha que queiramos aproximar a função de erro. Podemos usar uma aproximação local usando expansão de Taylor. A aproximação de primeira ordem seria:
E a de segunda ordem:
onde:
\(w = [w_{1},w_{2}]\)
\(w^{(0)} = [w_{1}^{(0)},w_{2}^{(0)}]\), são os valores pontuais
\(\left(w - w^{(0)} \right) = \begin{bmatrix} w_{1} - w_{1}^{(0)} \\ w_{2} - w_{2}^{(0)} \end{bmatrix}\) é um vetor coluna
\(\left(w - w^{(0)} \right)^{\top} = \begin{bmatrix} w_{1} - w_{1}^{(0)} & w_{2} - w_{2}^{(0)} \end{bmatrix}\) é um vetor linha
\(\nabla \mathcal{L}\vert_{w=w^{(0)}} = \begin{bmatrix} \frac{\partial \mathcal{L}}{\partial w_{1}}\vert_{w=w^{(0)}} \\ \frac{\partial \mathcal{L}}{\partial w_{2}}\vert_{w=w^{(0)}} \end{bmatrix}\)
Sendo \(\lambda\) a taxa de aprendizado, atualizaremos os valores de \(w\): \(w^{(1)} = w^{(0)} - \lambda \nabla \mathcal{L}\vert_{w=w^{(0)}}\). Substituindo eese novo valor em \(\mathcal{L}(w)\) temos:
O valor atualizado é a estimativa anterior, mais a melhora dada pelo gradiente e por último uma correção existente devido à curvatura.
No que se não houver curvatura o último termo é nulo e o gradiente sempre andará na direção de decréscimo do erro, assim podemos usar um \(\lambda\) tão grande quanto queiramos. O mesmo ocorre se o último termo for negativo.
A parte boa dessa aproximação é que caso o último termo seja positivo, podemos calcular o \(\lambda\) que minimiza o erro. Como? Com a derivada, é claro :)